Table of Contents
Sample Characterization
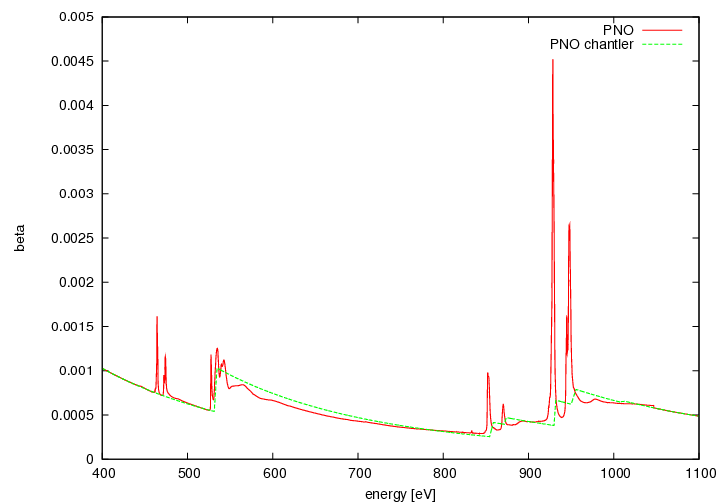
PNO: PrNiO3
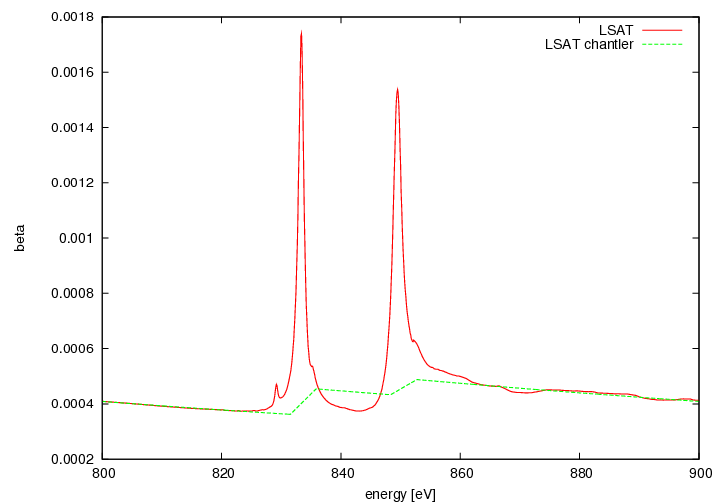
LSAT: 0.29(LaAlO3): 0.35(Sr2AlTaO6) (3.8735 Angstrom unit cell)
1)
Interesting peaks:
substrate:
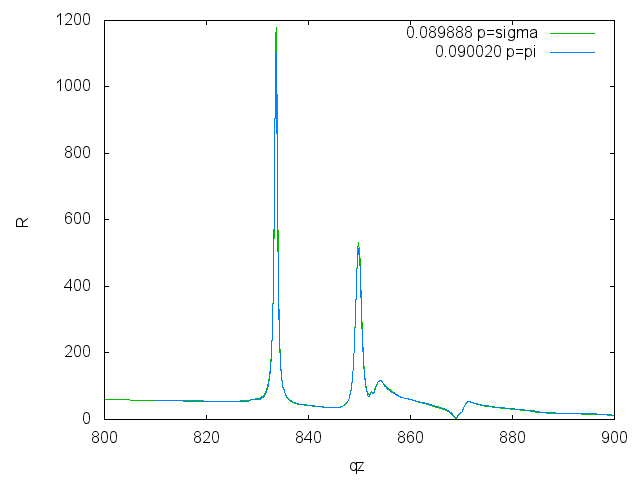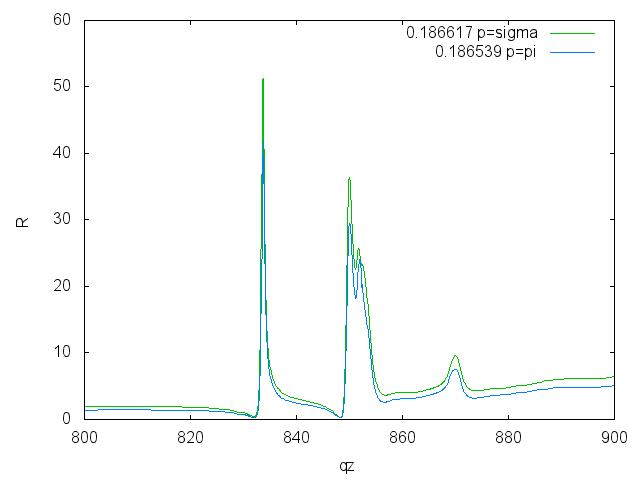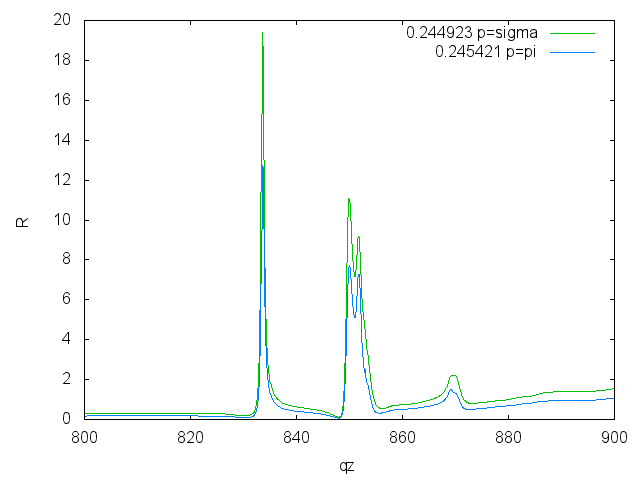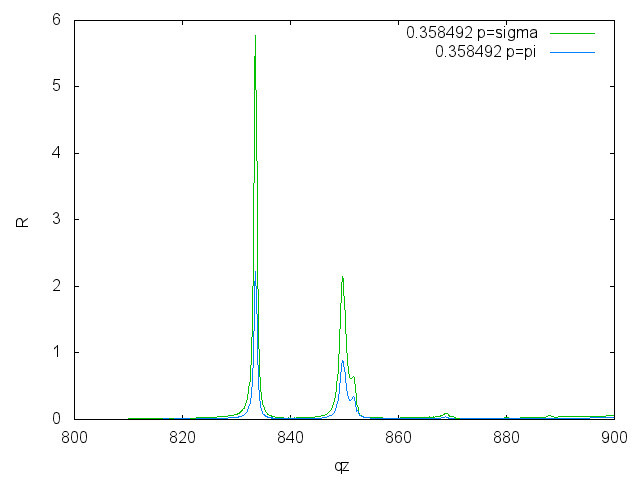
La M5: 836 eV
La M4: 853 eV
film:
Ni L3: 852.7 eV
Ni L2: 870.0 eV
Optical Constants
The TEY signals were fitted to chantler tables by the formula
beta(e) = alpha * TEY(e) / e + gamma + delta*e
e: energy
beta: imagninary part of the optical constant n as function of energy
TEY: measured TEY signal as function of energy
alpha, gamma, delta: fit parameters
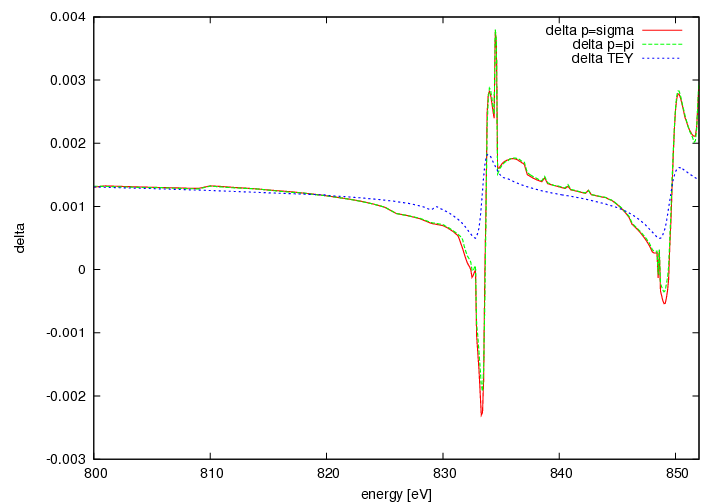
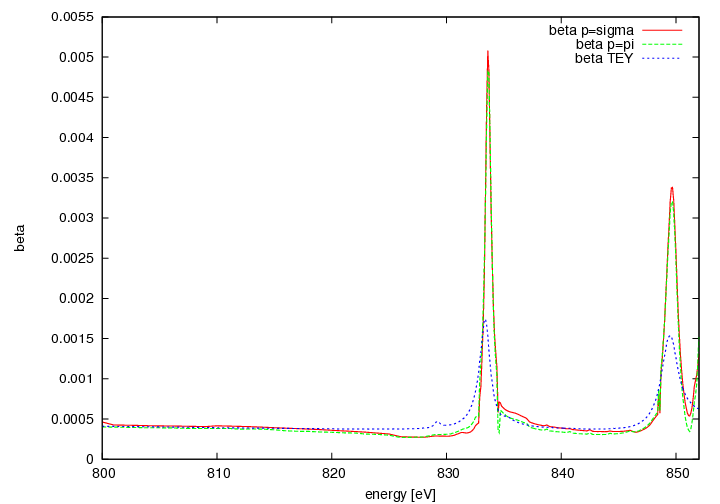
PNO
LSAT
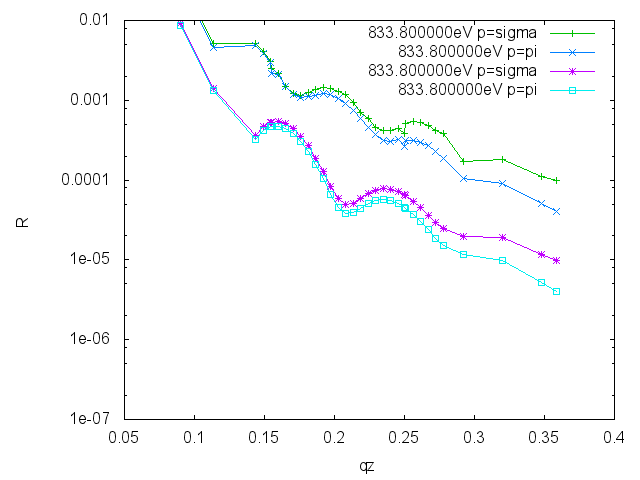
Reflectivities
At the REIXS beamline reflectivities, energy scans (const qz), and reflectity maps were measured. Putting all valid points together one can create a unsorted list
#energy qz Reflectivity polarization 800 0.143709769837871 8.0612174367649 v 801 0.143709858415225 8.05128038331844 v 802 0.143711236888019 8.03961449049679 v 803 0.143710416540384 8.03067803567478 v . . . 856.6 0.213303345314291 0.630505341022796 h 856.7 0.213302538170217 0.625630243774844 h 856.8 0.213303561368094 0.618766907338261 h . . . 870.5 0.172127894406649 5.64570582534484 h 870.5 0.175902024999232 6.58121875884301 h 870.5 0.17967280667221 7.14328792593677 h . . .
Writing a program to sort the data one can end up with very many reflectivies or escans
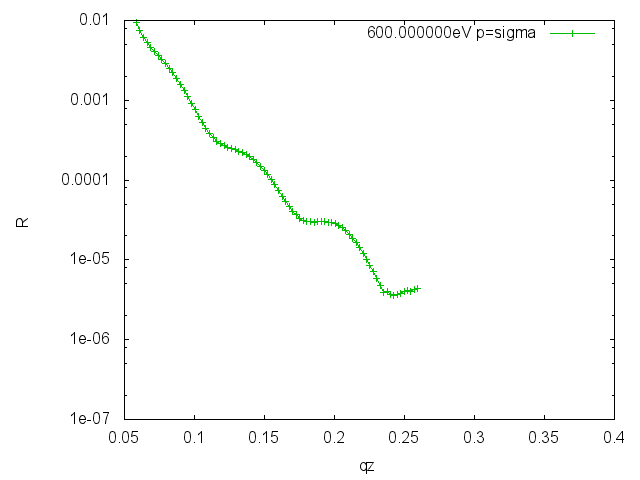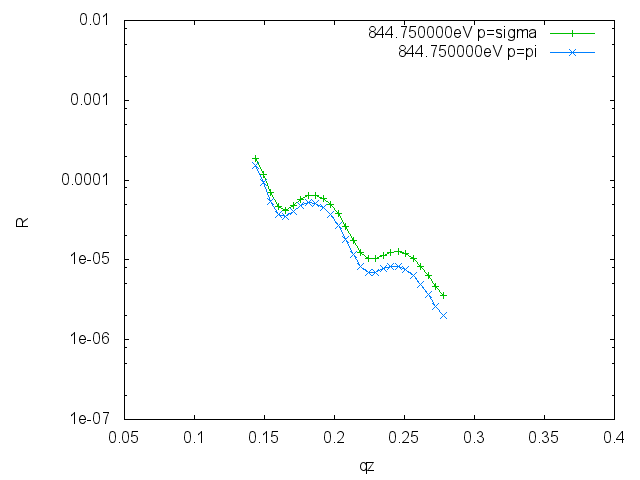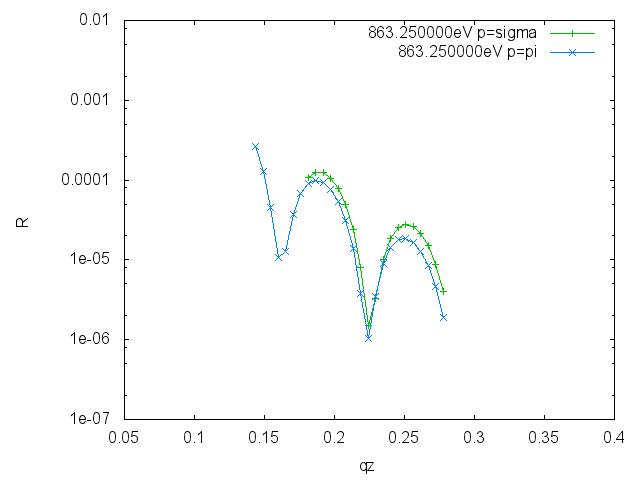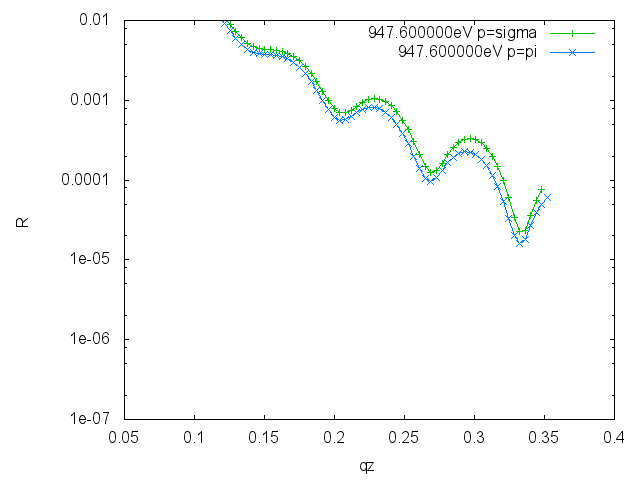
Reflectivities for both polarizations
Energy scans for both polarizations
Energy scans on Ni (pi correction)
To show the asymmetry between sigma and pi polarization one can multiply the pi-polarization by <m> cos(2theta)^2 </m>
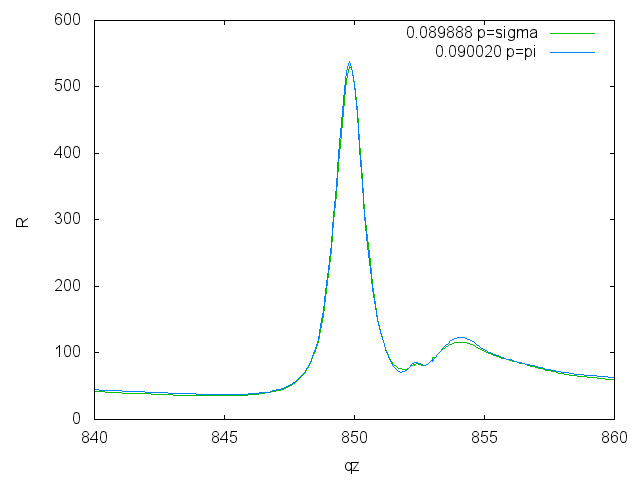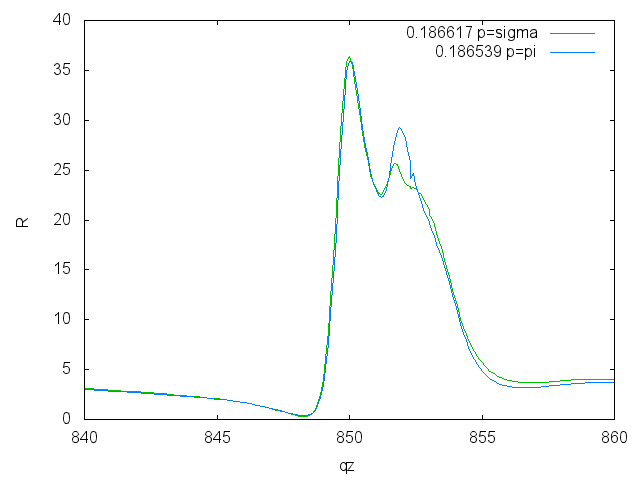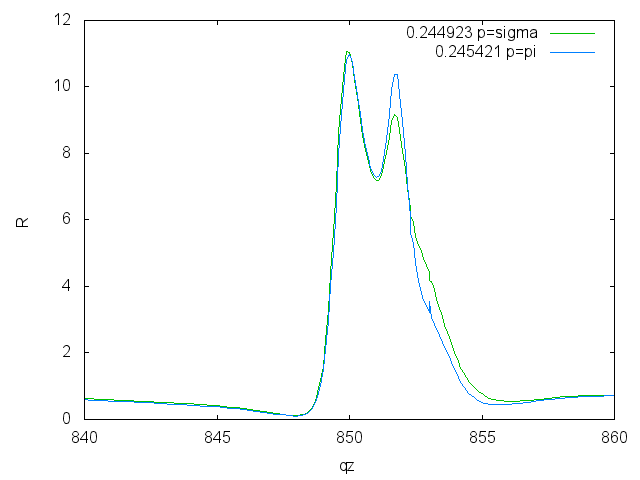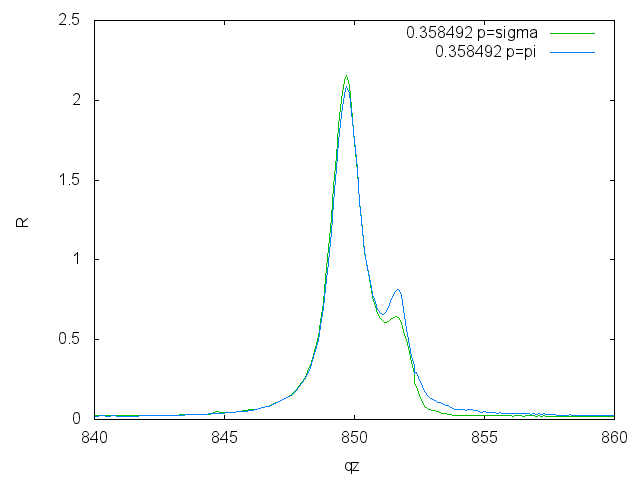
Fitting: An overview
Each of the reflectivities were fitted independently. The fit procedure was done with the simplex algorithm up to 500 iterations. For delta and beta, the tabulated values were taken.
Fitting thickness, interface roughness, surface roughness and multiplicator together
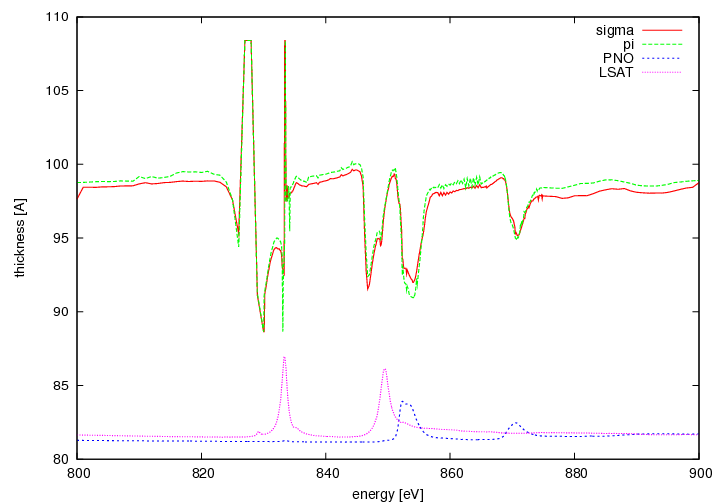
Thickness
- thickness around 90 to 100 Angstrom
- off resonant: thickness is constant (98 Angstrom)
- off resonant: thicker film of around 1 Angstrom for pi polarization
- La M5: left side of peak reduced thickness, right Ok
- La M4: left side of peak reduced thickness, right seems Ok
- Ni L3: reduced thickness, strong polarization dependent (vice versa to off-resonant)
- Ni L2: reduced thickness
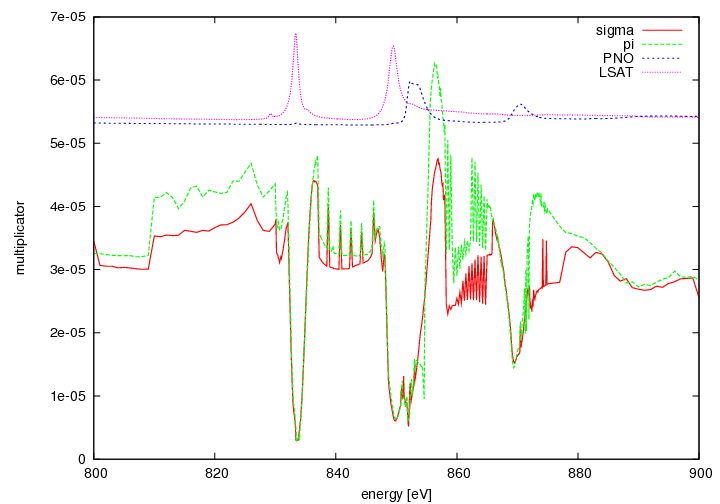
Multiplicator
- off resonant: factor around 3e-5
- strong influence on the number of points (peaks and noise effects). ⇒ Muliplicator can have a large error.
- almost a factor of 5 difference between off and on resonance
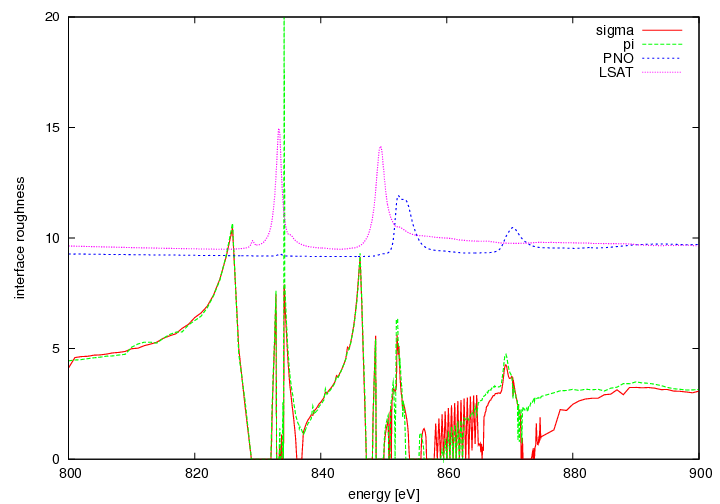
Interface roughness
- roughness varies between 0 and 10 Angstrom.
- off resonance: not constant
- off resonance: increasing with higher energy
- on resonance: sigma is often zero.
- depends on the number of points +- 2 Angstrom
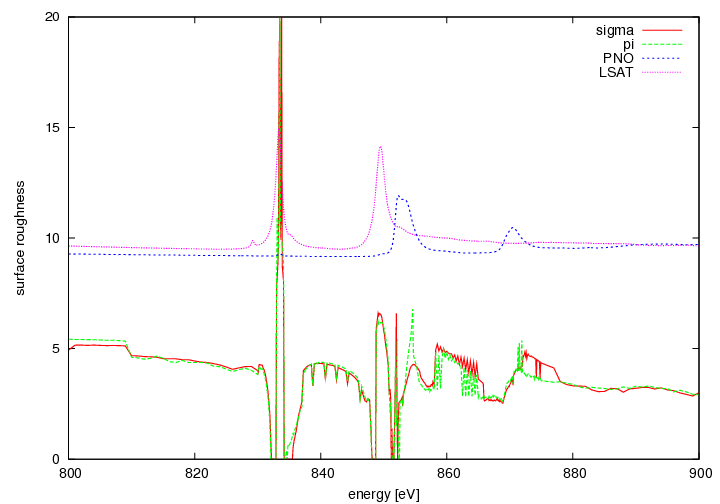
Surface roughness
- off resonance: surface roughness around 3-5 Angstrom
- on resonance: roughness can drop to zero
- depends on the number of points +- 1 Angstrom
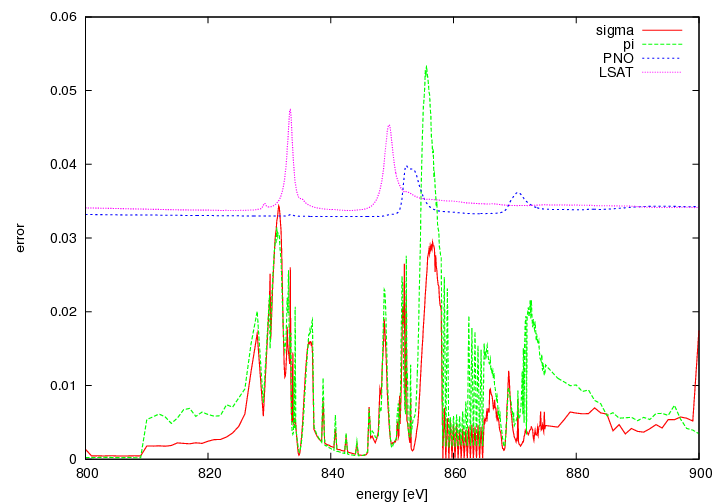
Error of fit
Fitting: Refining
- Set multiplicator. This must be constant in that range. Off resonant fit very well, so choose 3e-5 as multiplicator.
- set maximum roughness of the surface to 7 Angstrom
Fitting thickness, interface roughness, surface roughness together
This gives almost the same results as the first fit. But the error changes especially on resonant on the La-edges,.
- the top two curves are the measurement, the bottom two curves are the fit.
Fitting: Optical constants
- Fixed thickness to 98.5 Angstrom
- Fit delta and beta of substrate independently ( no Kramers-Kronig relation)
Fitting interface roughness, surface roughness and delta, beta of LSAT
delta and beta
- huge underestimate of the size of peaks. (The La peak of LAO is not really a good replacement)
- almost no difference between sigma and pi
- off resonant fits very well with chantler tables
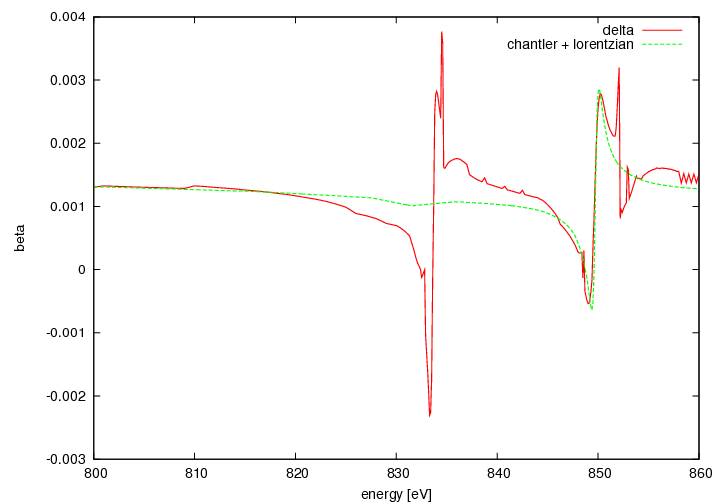
Apply Kramers-Kronig
- Because of the disturbance of the Ni L3 edge one has to fit a lorentzian to the La M4 edge and take this values for the higher energies (850-860 eV).
Fit Lorentzian to the M4 peak
- take the new values for delta and beta and put them to chantler.
- calculate Kramers-Kronig beta→delta and delta→beta